Uniform Point Distributions for Surfaces and Volumes
3/27/2025 / 4 minutes to read / Tags: guide, math, geometry, computer-graphics
This article is currently a work in progress, come back later!
Flipping points outside of the unit triangle back inside
Mapping points to triangle space
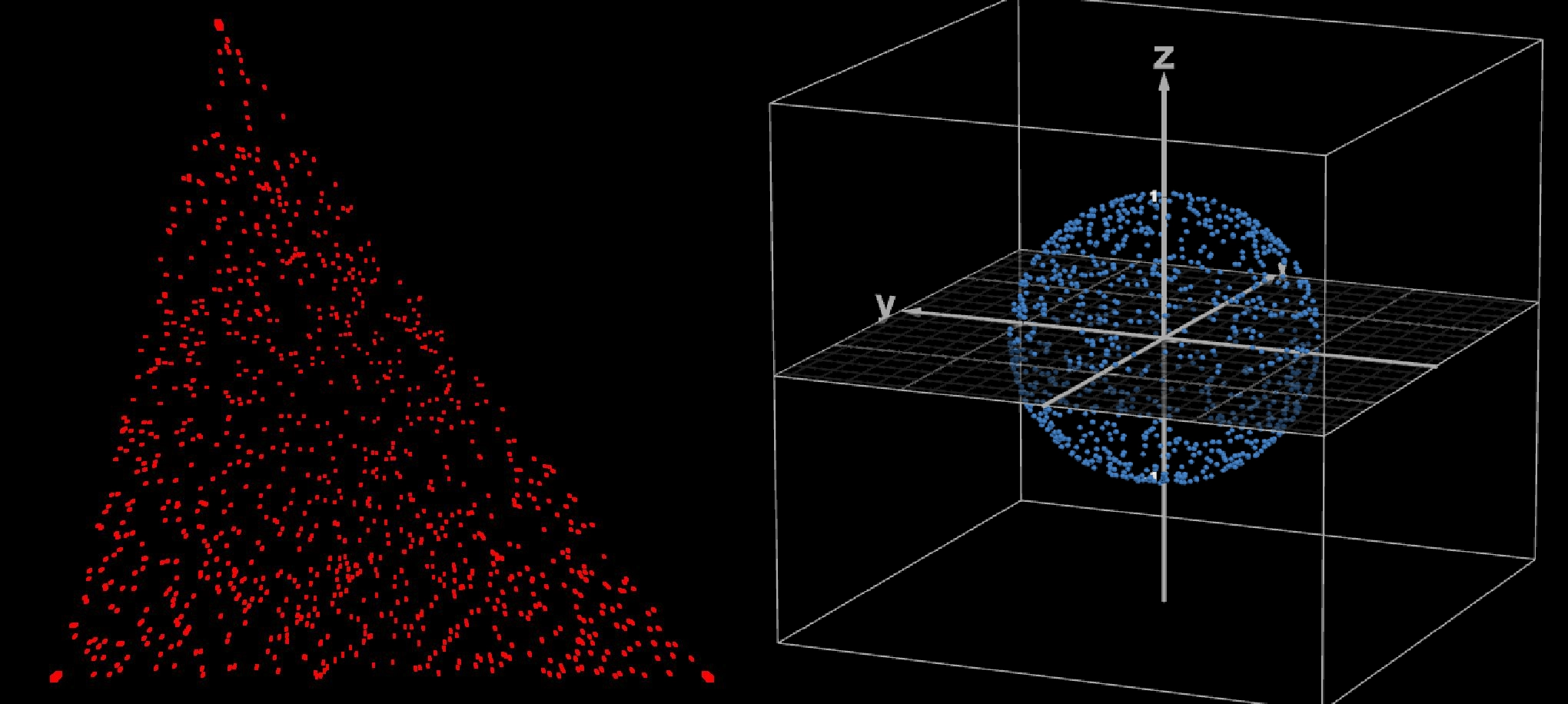
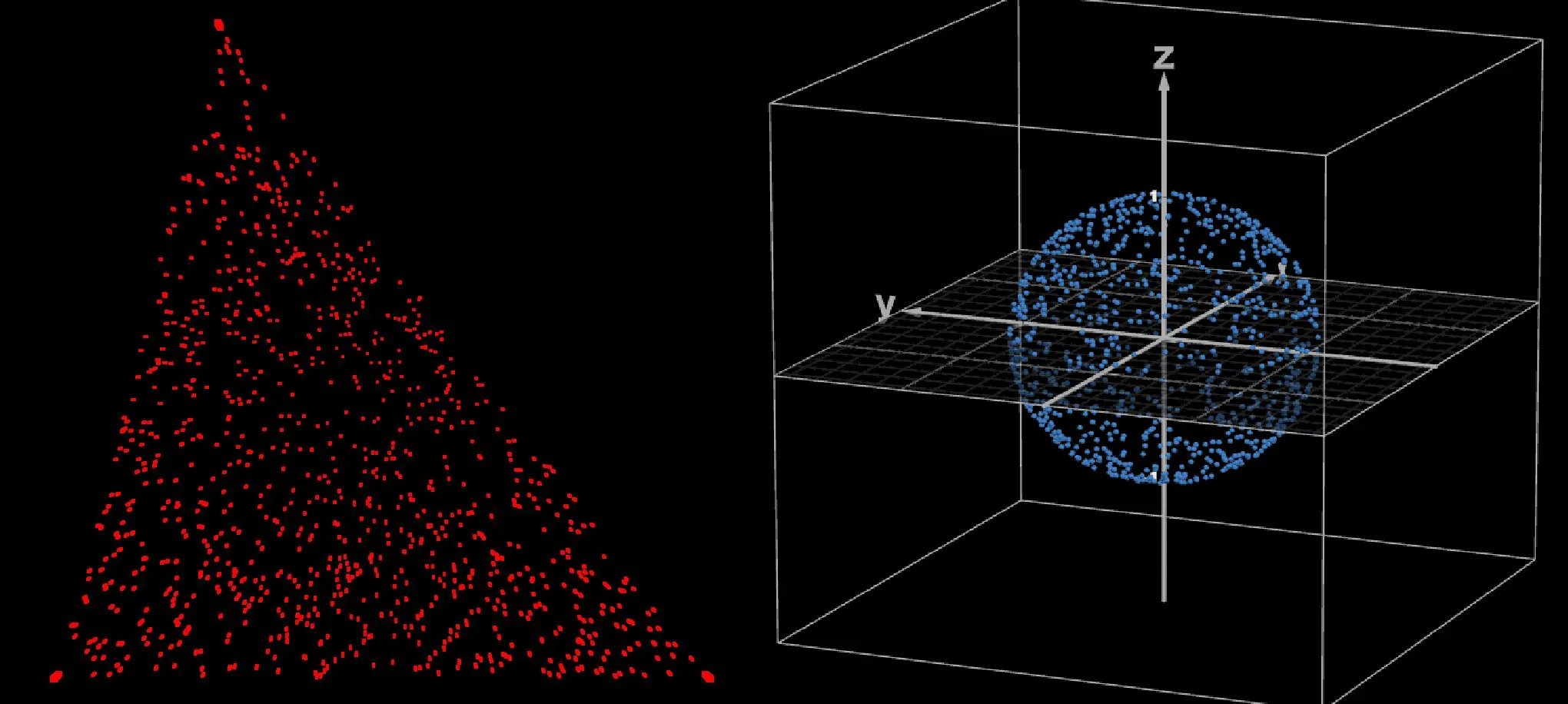
2D
3D
let sampleNormalDistribution = () => { // Using the Box-Muller transform to generate a normal distribution let u = Math.random(); let v = Math.random(); let r = Math.sqrt(-2 * Math.log(u)); let theta = 2 * Math.PI * v; return r * Math.cos(theta);}
let positions = [];for ( let i = 0; i < 1000; i ++ ) { let x = sampleNormalDistribution(); let y = sampleNormalDistribution(); let z = sampleNormalDistribution(); let magnitude = Math.sqrt(x * x + y * y + z * z); x /= magnitude; y /= magnitude; z /= magnitude; positions.push(x); positions.push(y); positions.push(z);}If you want to generate a random distribution of points throughout the sphere instead, sample again, this time with a uniform distribution between [0,1], cube root the value, and multiply by the previous value. This will give you a uniform distribution of points throughout the sphere.
let sampleNormalDistribution = () => { ... }
let positions = [];for ( let i = 0; i < 10000; i ++ ) { let x = sampleNormalDistribution(); let y = sampleNormalDistribution(); let z = sampleNormalDistribution(); let r = Math.cbrt(Math.random()); // Cube root! Not square root let magnitude = Math.sqrt(x * x + y * y + z * z); x *= (r / magnitude); y *= (r / magnitude); z *= (r / magnitude); positions.push(x); positions.push(y); positions.push(z);}← Back to blog